Global matrix representation

The global matrix representation is simply the bundle of the matrix equations for solving a force constants. It can be accepted that the force constants are solved separately. We enjoy the benefit of the global solution when we consider translational invariance. The global matrix equation is constructed as follows,

$$\begin{multline} \mathbf{F} \begin{pmatrix} \mathbf{F}_{1, 1} \\ \vdots \\ ... ...f{P}_{n_{\mathrm{unit}}, n_{\mathrm{super}}} \\ \end{pmatrix}, \end{multline}$$

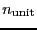where $n_{\mathrm{unit}}$ is the displaced atom number in unit cell and $n_{\mathrm{super}}$ is the atom number in supercell where the force is measured. Due to crystal symmetry, the number of displaced atoms and the number directions may be reduced. The number of the operations to symmetrize force constants may be increased. The number of atoms and symmetry operations affect to the size of global matrix significantly and they dominate the size of memory allocation in computation. Finally, solving following equation,

$$\mathbf{P} = - \mathbf{U}^{-1} \cdot \mathbf{F},$$ (3.8)

we know all force constants at the same time.