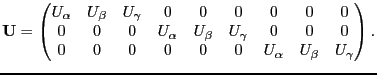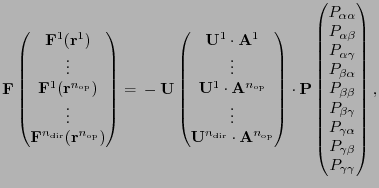A displacement is represented as
 matrix for easy
treatment as shown in below,
matrix for easy
treatment as shown in below,
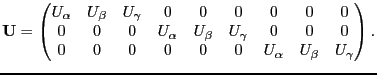 |
(3.3) |
First we must know the site point symmetry of the atom which is
displaced. To symmetrize force constants, similarity
transformation [12] is used like,
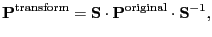 |
(3.4) |
where
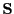 is a site point symmetry operation where the
transformation center is on the displaced atom and is
is a site point symmetry operation where the
transformation center is on the displaced atom and is
 matrix. In this equation, force constants are treated as
matrix. In this equation, force constants are treated as
 matrix. After transformation, force constants are converted to
matrix. After transformation, force constants are converted to
 matrix. The position of
atom
matrix. The position of
atom
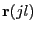 is also translated to
is also translated to
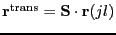 . These
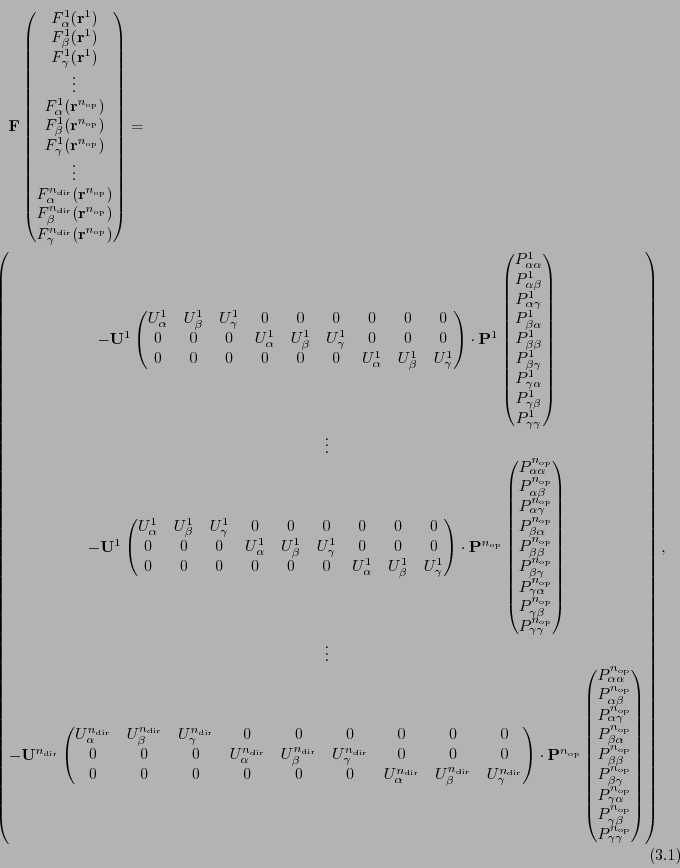
matrices are connected in one matrix equation as follows,
. These
matrices are connected in one matrix equation as follows,
where, the sufficient number of directions where the atom is displaced are
denoted as
 and the number of the site point
symmetry operations are denoted as
and the number of the site point
symmetry operations are denoted as
 . At this point,
force constants are unknown, but symmetry operations are known. In
this case, the symmetry operation should be done to displacement
matrices rather than to force constants. Therefore the symmetry
operations are separated from transformed force constants and the
separated symmetry properties are connected to the displacement
matrices as follows,
. At this point,
force constants are unknown, but symmetry operations are known. In
this case, the symmetry operation should be done to displacement
matrices rather than to force constants. Therefore the symmetry
operations are separated from transformed force constants and the
separated symmetry properties are connected to the displacement
matrices as follows,
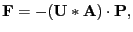 |
(3.5) |
where
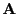 is the symmetry property matrix which is determined
by rule. The operation '
is the symmetry property matrix which is determined
by rule. The operation '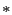 ' represents the operation between
' represents the operation between
 and
and
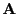 . This equation is described as,
. This equation is described as,
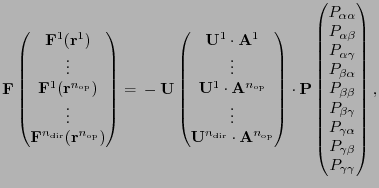 |
(3.6) |
where
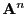 is
is
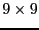 symmetry property matrix.
symmetry property matrix.
This equation can be solved by matrix inversion, as shown below,
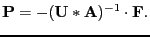 |
(3.7) |
In most cases, force constants
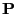 are over-determined. In
fropho, the least-squares solution of force constants is calculated by
using singular value decomposition [13] in LAPACK
routine [16].
are over-determined. In
fropho, the least-squares solution of force constants is calculated by
using singular value decomposition [13] in LAPACK
routine [16].
togo
2009-02-12