Calculating forces, we need to introduce finite displacements to each
atom in unit cell. In principle, we need number of displacements of
freedom. In the case that target crystal model has crystal symmetry
operations more than two, the number of displacements are
reduced. Using sufficient forces and displacements, we will create
force constants. In fropho, force constants are calculated as follow,
 |
(3.1) |
where 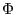 is force constant,
is force constant,  and
and  are independent
directions which are arbitrarily chosen,
are independent
directions which are arbitrarily chosen,
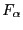 is force of
is force of
 direction and
direction and
 is displacement of
is displacement of  direction.
direction.  denotes an atom in the
denotes an atom in the  -th unit cell. Symmetry
operations also symmetrize the force constants. Therefore a force
constant matrix should be connected to another one. To do so, group
theory is employed for sophisticated symmetrization. In fropho, which
is not sophisticated, symmetry operations derived from crystal
symmetry are used for symmetrize them 'numerically'.
-th unit cell. Symmetry
operations also symmetrize the force constants. Therefore a force
constant matrix should be connected to another one. To do so, group
theory is employed for sophisticated symmetrization. In fropho, which
is not sophisticated, symmetry operations derived from crystal
symmetry are used for symmetrize them 'numerically'.
Usually force constants are treated as
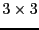 matrix. In fropho
code, when generating force constants, this is treated as
matrix. In fropho
code, when generating force constants, this is treated as
 matrix. This treatment has a good point that we can know all the force
constants at the same time by solving linear equation of a matrix. In
the following sections, I will describe how to construct matrices and
how to solve it.
matrix. This treatment has a good point that we can know all the force
constants at the same time by solving linear equation of a matrix. In
the following sections, I will describe how to construct matrices and
how to solve it.
Subsections
togo
2009-02-12


![]() matrix. In fropho
code, when generating force constants, this is treated as
matrix. In fropho
code, when generating force constants, this is treated as
![]() matrix. This treatment has a good point that we can know all the force
constants at the same time by solving linear equation of a matrix. In
the following sections, I will describe how to construct matrices and
how to solve it.
matrix. This treatment has a good point that we can know all the force
constants at the same time by solving linear equation of a matrix. In
the following sections, I will describe how to construct matrices and
how to solve it.